1.2. Vectors
Vectors in 2D and 3D space
Vectors
Vector and points are both lists of three numbers so there’s absolutely no way of telling whether it is a point or a vector.
A vector is an arrow in space which always starts at the world origin (0, 0, 0) and ends at the specified coordinate.
A vector is a quantity that describes Direction and Magnitude.
2D Vectors
A 2D vector can be specified in the following way as a matrix:
$$\overrightarrow{v} = \begin{bmatrix}
x_1 \\
y_2
\end{bmatrix}$$
$$\overrightarrow{v} = \begin{bmatrix}
2 \\
3
\end{bmatrix}$$
or as a list:
$$\overrightarrow{v} = \begin{bmatrix} 2, 3 \end{bmatrix}$$
3D Vectors
A 3D vector can be specified in this way as a matrix:
$$\overrightarrow{v} = \begin{bmatrix}
x_1 \\
y_1 \\
z_1
\end{bmatrix}$$
$$\overrightarrow{v} = \begin{bmatrix}
2 \\
3 \\
3
\end{bmatrix}$$
or as a list:
$$\overrightarrow{v} = \begin{bmatrix} 2, 3, 3 \end{bmatrix}$$
Operations with vectors
Addition
The sum of two vectors is a third vector, represented as the diagonal of the parallelogram constructed with the two original vectors as sides.
$$\overrightarrow{AB} = \begin{bmatrix}
a1 \\
a2 \\
a3
\end{bmatrix}
+\begin{bmatrix}
b1 \\
b2 \\
b3
\end{bmatrix}
= \begin{bmatrix}
a1+b1 \\
a2+b2 \\
a3+b3
\end{bmatrix}
$$
Multiplication
When a vector is multiplied by a positive scalar (i.e., number), its magnitude is multiplied by the scalar and its direction remains unchanged (if the scalar is negative, the direction is reversed).
$$\overrightarrow{v} = \begin{bmatrix}
a1 \\
a2 \\
a3
\end{bmatrix}
3
= \begin{bmatrix}
a1 \cdot 3 \\
a2 \cdot 3 \\
a3 \cdot 3
\end{bmatrix}
$$
Vector multiplication: The vector is now half its original size (multiplied by 0.5).
Magnitude
The magnitude of a vector is its size. It can be calculated from the square root of the total of the squares of of the individual vector components.
Normalization
To normalize a vector, therefore, is to take a vector of any length and, change its length to unit 1, turning it into what is called a unit vector. Since it describes a vector’s direction without regard to its length, it’s useful to have the unit vector readily accessible.
Dot product
The multiplication of a vector A by another vector B leads to the dot product (also known as scalar product), returning a number.
The dot product of two vectors can be defined as the product of the magnitudes of the two vectors and the cosine of the angle between the two vectors.
Alternatively, it is defined as the product of the projection of the first vector onto the second vector and the magnitude of the second vector.
$$ A \cdot B = |A| |B| cos (\alpha)$$
The dot product essentially tells us how much of the force vector is applied in the direction of the motion vector.
The dot product can also help us measure the angle formed by a pair of vectors and the position of a vector relative to the coordinate axes. This being able to be positive, negativ or equal to 0 (if both vectors are ortogonal)
Cross product
Also called the vector product of two vectors A (Red) and B (Green), resulting a third vector C (Blue), perpendicular (Normal Vector) to the plane of the original vectors (A and B). Its magnitude is given by the area of the parallelogram between A and B, and its direction can be determined by the right-hand thumb rule (See bellow).
$$ A \times B = |A| |B| sin (\alpha) $$
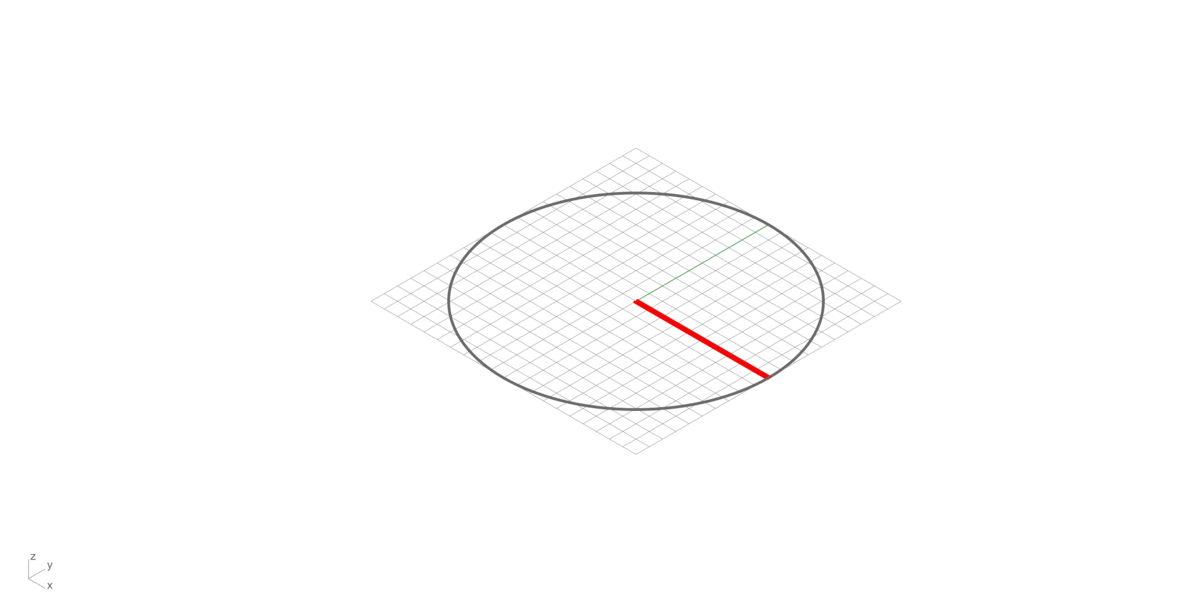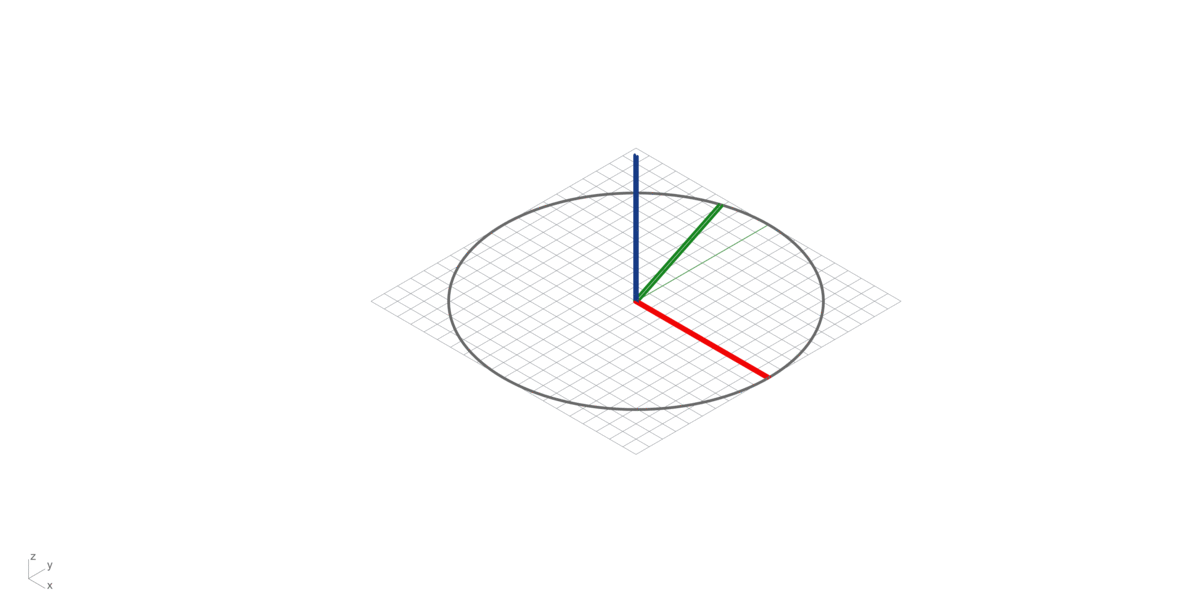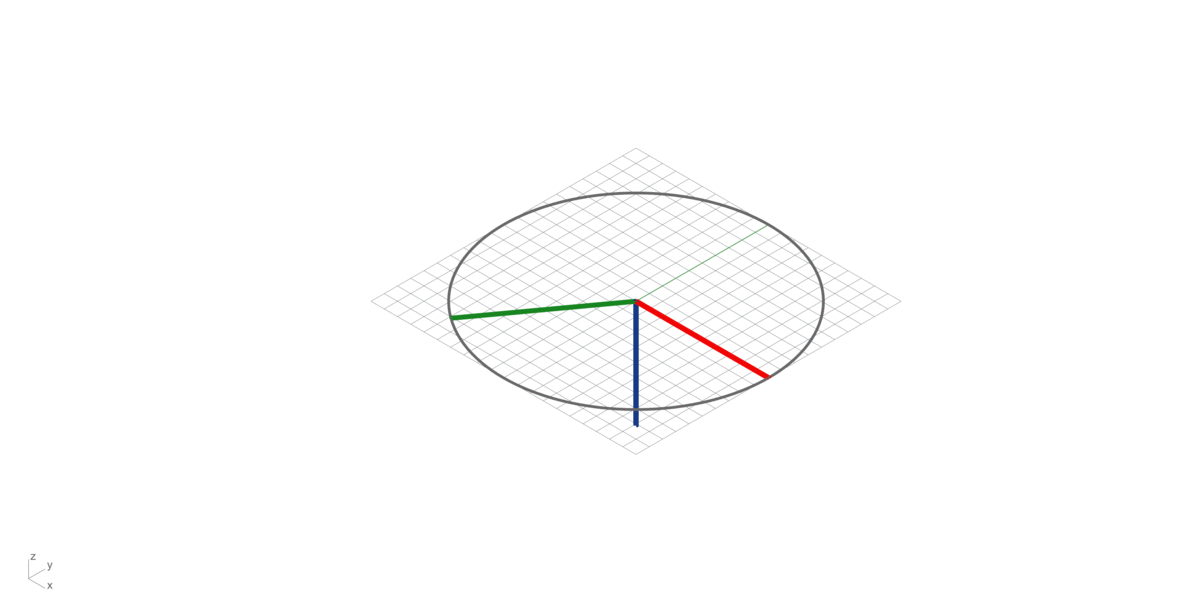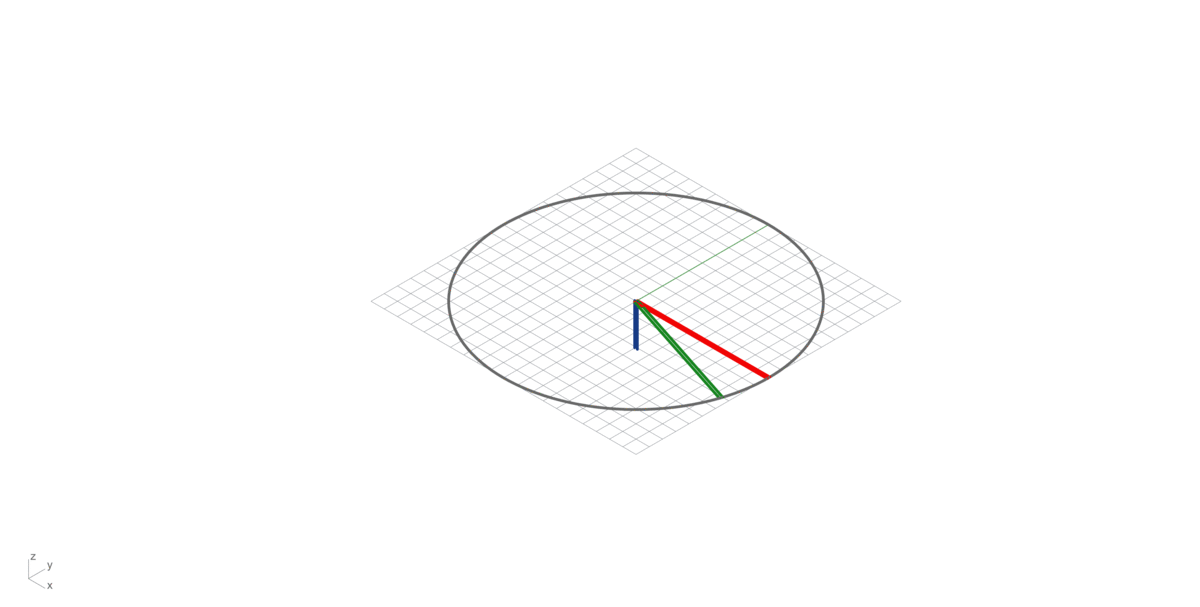
Right-hand rule
Right-hand rule is a common mnemonic for understanding orientation of axes in three-dimensional space. This will help you in remembering the direction of the third vector resulting from a Cross Product multiplication of two vectors.